
Бином Ньютона
Треугольник Паскаля

Бином Ньютона

Евклид
325 года до н. э -
265 года до н. э
Древние Афины
Научная работа, в которой рассмотрена формула
«Начала», II книга
Название формулы в работе ученого, краткое ее описание
Формулировка частного случая бинома для показателя 2:
Предложение IV
«Ежели прямая линия рассечена как ни есть, то квадрат из целой равен квадратам из отрезков и вместе дважды взятому прямоугольнику, содержимому в сих отрезках.»
(а+b)2=a2+2ab+b2
Дополнительная
информация
У древних греков величины обозначались не числами или буквами, а отрезками прямых. Они говорили не «а», а «квадрат на отрезке а», не «аb», а «прямоугольник, содержащийся между отрезками а и b ».

Научная работа, в которой рассмотрена формула
«Чандас-шастра» (Chandahsutra) или «Чандас-сутра»
Ачарья Пингала
II в. до н. э -
(около 150 г. до н.э.)
Древняя Индия
Название формулы в работе ученого, краткое ее описание
В своем труде спрашивал, сколькими способами можно составить шестисложный метр из коротких и длинных нот.
Пингала находил количество метров, в которых n- длинные слоги и k- короткие слоги. Это считают эквивалентно нахождению биномиальных коэффициентов.

Научная работа, в которой рассмотрена формула
"Арифметика"
Диофант Александрийский
III в. н. э
Древняя Греция
Александрия
Название формулы в работе ученого, краткое ее описание
В своей книге «Арифметика» Диофант первым ,формулы квадрата суммы, квадрата разности и разности квадратов рассматривал с арифметической точки зрения, уходя от принятых геометрических способов
Дополнительная
информация
Научная работа, в которой рассмотрена формула
Халаюдха
X век
Индия
«Комментарии к «Чандас-шастра»Пингала»
(около 960г)
Название формулы в работе ученого, краткое ее описание
Первое упоминание треугольной последовательности биномиальных коэффициентов под названием «Лестница на гору Меру»( meru-prastaara)
«После построения квадрата на вершине ниже строятся еще два квадрата так, чтобы половина каждого располагалась под каждой из двух сторон. Затем построим три квадрата, еще ниже - четыре квадрата; процесс повторяется до тех пор, пока требуемая пирамида не будет получена. В первом квадрате запишем 1; в каждом из 2-х квадратов второй линии снова поместим по единице. В последующих линиях единицу поместим в каждом из 2-х крайних квадратов, а в средних квадратах помещаем сумму цифр ближайших двух квадратов, расположенных выше. Т.о. заполняют все квадраты. Тогда вторая линия даст число комбинаций из короткого и длинного звуков, образующих один слог; третья даст то же самое для 2-х слогов, четвертая для 3-х слогов и т.д»
Дополнительная
информация


Абу Бакр
аль-Караджи
953-1029
Персия
Научная работа, в которой рассмотрена формула
«Книга об алгебре и алмукабале»
1010г
Название формулы в работе ученого, краткое ее описание
Для суммы квадратов аль-Караджи приводит верную формулу, но сообщает, что доказать её правильность он не может.
Для суммы кубов он приводит геометрическое доказательство.
Так же Аль-Караджи приводит в своём сочинении таблицу биномиальных коэффициентов.
Дополнительная
информация
Научная работа, в которой рассмотрена формула
Цзя Сянь
1010–1070
Китай
"Ши Суо Суан Шу "
(около 1050-1060)
Название формулы в работе ученого, краткое ее описание
Составил треугольную таблицу биномиальных коэффициентов до n = 6 (треугольник Цзя Сянь). Цзя использовал его как инструмент для извлечения квадратных и кубических корней.
Дополнительная
информация

Омар Хайям
1048- 1131
Персия
Научная работа, в которой рассмотрена формула
трактат
«Трудности арифметики»
Название формулы в работе ученого, краткое ее описание
По мнению исследователей Б.А. Розендельда и А.П. Юшкевича, в этой работе Омар Хайям первым в истории математики предложил общий прием извлечения корней n-й степени из чисел, основанный на знании формулы n-й степени двучлена
Дополнительная
информация
Научная работа, в которой рассмотрена формула
Аль-Самаваль
аль-Магриби
1130–1180
Иран
«Аль-Бахир фил-джабр»
перевод
«Блестящий в алгебре»
1149г
Название формулы в работе ученого, краткое ее описание
Доказывается биномиальную теорему для n = 3, 4, 7, и приводится таблица нахождения биномиальных коэффициентов
Дополнительная
информация
Научная работа, в которой рассмотрена формула
Ян Хуэй
1238–1298
Китай
«Сянцзе цзючжан суаньфа»
перевод
«Подробное разъяснение методов исчисления в девяти разделах»
1261г
Название формулы в работе ученого, краткое ее описание
Самая ранняя сохранившаяся китайская иллюстрация « Треугольника Паскаля» на ней шестистрочный треугольник для расчета (а + b)6
Автор писал: «Мой метод нахождения квадратных и кубических корней был основан на методе Цзя Сянь из Ши Суо Суан Шу »
Дополнительная
информация
Страница из энциклопедии Юнлэ сохранила этот исторический факт.

Насир ад-Дин Туси
1201- 1274
Персия
Научная работа, в которой рассмотрена формула
«Сборник по арифметике с помощью доски и пыли»
1265г.
Название формулы в работе ученого, краткое ее описание
Приводит таблицу биномиальных коэффициентов в форме треугольника до n=12
Дополнительная
информация
Научная работа, в которой рассмотрена формула
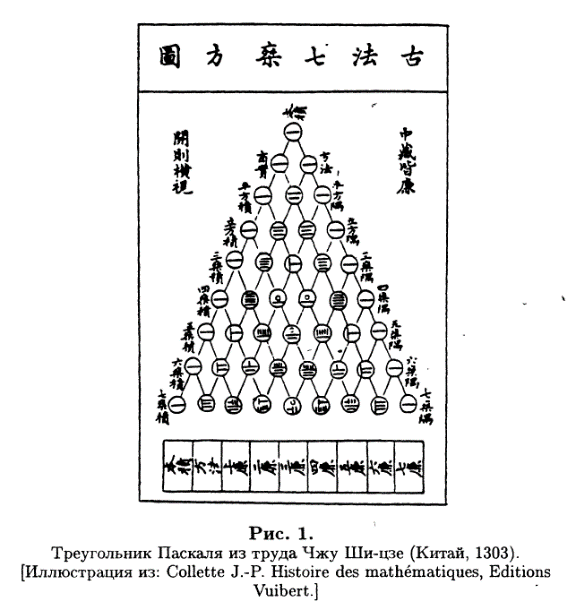
Чжу Шицзе
1249–1314
Китай
«Яшмовое зеркало четырёх первоэлементов»
1303
Название формулы в работе ученого, краткое ее описание
Изображение треугольника Паскаля на одной из иллюстраций, дополненного до восьми строк
Дополнительная
информация
Научная работа, в которой рассмотрена формула
Нараяна Пандита 1325–1400
Индия
"Ганита Каумуди"
перевод
"Освещенный «Лунный свет математики»"
13 глава Анка-паша (Aṅka-pāśa )
Название формулы в работе ученого, краткое ее описание
В 13 главе среди 97 правил и 45 примеров, математик рассмотрел вычисление биноминальных коэффициентов.
Дополнительная
информация

Джамшид аль-Каши
1380-1429
Иран
Научная работа, в которой рассмотрена формула
«Ключ к арифметике»
Пятая книга: о нахождении неизвестных с помощью алгебры и алмукабалы
1427
Название формулы в работе ученого, краткое ее описание
Разложение Бинома Ньютона для любого натурального показателя.
Дополнительная
информация

Петер Биневиц
1495-1552
Германия
Научная работа, в которой рассмотрена формула
«Новое и хорошо обоснованное наставление по арифметике для всех купцов» Справочник по коммерческой арифметике
1527г.
Название формулы в работе ученого, краткое ее описание
В этом справочнике впервые в печати появилась таблица биноминальных коэффициентов
Дополнительная
информация

Михаэль Штифель
1487-1567
Германия
Научная работа, в которой рассмотрена формула
«Обобщённая арифметика» Arithmetica integra
1544
Название формулы в работе ученого, краткое ее описание
Многомерное обобщение куба используется М.Штифелем в 1553г. для иллюстрации формулы бинома, которую он формулирует для любого натурального показателя.
М.Штифель ввёл термин «биномиальный коэффициент» и приводит таблицы биномиальных коэффициентов до 18 степени, где каждый элемент образуется как сумма элементов предыдущей строки, стоящих над ним и слева от него: «Так же как квадратные биномы разлагаются на 4 части, а кубические – на 8 частей, квадрато-квадратные биномы разлагаются на 16 частей, а сверхтелесные на 32 части и подобно этому идет по двукратной прогрессии»
Дополнительная
информация

Никколо Тарталья
1499-1557
Италия
Научная работа, в которой рассмотрена формула
"Общий трактат о числе и мере" ч.1-6
(«Generale trattato de numeri e misure»)
1556-1560
Название формулы в работе ученого, краткое ее описание
Придал таблице биноминальных коэффициентов следующий вид:

Здесь каждое число является суммой чисел, стоящих перед ним и над ним, а коэффициенты различных степеней бинома расположены по диагоналям, соединяющим числа первого столбца с числами первой строки, имеющими тот же порядковый номер.
Дополнительная
информация
Научная работа, в которой рассмотрена формула
Рафаэль Бомбелли
1526-1572
Италия
Название формулы в работе ученого, краткое ее описание
Приведено разложение бинома до n=7, используя коэффициенты при вычислении соответствующих корней
Дополнительная
ин�формация


Йоганн Фаульгабер
1580-1635
Германия
Научная работа, в которой рассмотрена формула
Название формулы в работе ученого, краткое ее описание
Приведены без доказательства значения для суммы степеней m первых восьми чисел натурального ряда, где m = 1, 11
Дополнительная
информация

Блез Паскаль
1623-1662
Франция
Научная работа, в которой рассмотрена формула
Название формулы в работе ученого, краткое ее описание
Исследует свойства биномиальных коэффициентов при возвышении бинома в любую целую положительную степень (частный случай бинома Ньютона). Паскаль находит их, впервые в истории математики сознательно применяя метод полной математической индукции, — способ рассуждения от n к n+1.

Дополнительная
информация


Научная работа, в которой рассмотрена формула
письмо графу Г.Ольдербургу и Г.В. Лейбницу
1676г
Исаак Ньютон
1642-1727
Англия
Название формулы в работе ученого, краткое ее описание
Получил формулу в период 1664-1665г.
В письме указывает общее биноминальное разложение в виде:


В последующих письмах Ньютон приводит свою формулу к современному виду:
Дополнительная
информация

Научная работа, в которой рассмотрена формула
«Универсальная арифметика" Том первый, содержащий в себе все образы алгебраического вычисления
1768
Леонард Эйлер
1707-1783
Швейцария/
Россия
Название формулы в работе ученого, краткое ее описание
Во втором разделе, озаглавленном "О разных исчислениях составных количеств", исследует бином Ньютона для рациональных чисел, обобщает формулу и выводит тождество:

Дополнительная
информация


Научная работа, в которой рассмотрена формула
журнал «Journal für die reine und angewandte Mathematik» или «Crelle's Journal»
№1-1826г
Нильс Хенрик
Абель
1802-1829
Норвегия
Название формулы в работе ученого, краткое ее описание
Исследовал биноминальный ряд. Вывел «Биномиальную теорему Абеля», которая является математическим тождеством с участием суммы из биномиальных коэффициентов

Дополнительная
информация
На протяжении веков люди интересовались математическими знаниями. Любое важное открытие в математике строится на работах предшественников и исследователях, на их долгом и часто безызвестном труде. И. Ньютон в письме Роберту Гуку писал: «Если я видел дальше других, то потому, что стоял на плечах гигантов». В истории открытия биноминальной теоремы таких гигантов было множество, начиная с древних времен: Эвклид, Халаюдха, Абу Бакр аль-Караджи и многие другие. Но обязательно должен быть человек, у которого, получается, объединить разрозненные знания. В нашем случае этим человеком является Исаак Ньютон, чье имя по праву носит обобщённая формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных.
В разных странах формула «Бином Ньютона» называется по-разному:
1) Binomial formula, binomial theorem - Англия
2) Newtonsches Binomo- Германия
3) Binôme de Newton, théorème binomial- Франция
4)Binomická věta-Чехия
5) Teorema del binomio –Испания
Бином Ньютона применяется в решение задач в области комбинаторики, математической статистики и логики, в исследовании функций и приближённых вычислений.

